IMod header

IMod – Partial differential equations, statistics and data:
An interdisciplinary approach to data-based modelling

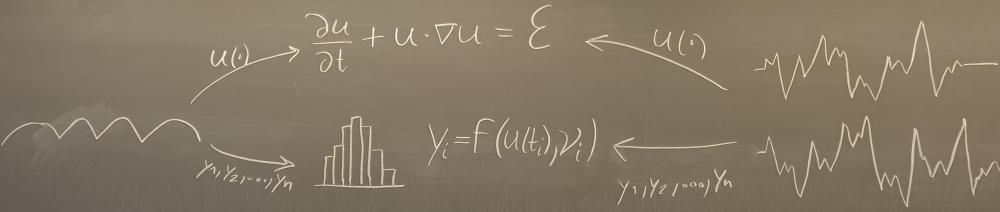
Schematic description of project. Chalk on blackboard.

IMod main content

 

IMod is an interdisciplinary project for building, analysing and testing a framework for data-based modelling built on the combination of partial differential equations and statistical modelling, and applied in particular to surface fluid mechanics and neuroscience.

The primary objective of IMod is to develop a novel mathematical-statistical framework for data-driven models of complex systems, guided by problems in fluid mechanics and neuroscience.

Scientific description.

IMod research goals

IMod research goals

  1. Combine partial differential equations and statistical theory to develop models with uncertainty for capturing interactions in complex systems.
  2. Create effective and fast methods to identify physical parameters from sparsely observed phenomena.
  3. Rigorously study the systems from a mathematical and physical viewpoint.
  4. Unite theory and data to develop models in fluid mechanics and neuroscience using tailor-made experiments.

Principal investigators (IMod)

Principal investigators

Mats Ehrnstrom
Mats Ehrnstrom
Project manager / PI

Project Partners (IMOD)

Project partners

José Antonio Carrillo
Professor
University of Oxford
Stefano Castruccio
Associate Professor
University of Notre Dame
Flavio Donato
Professor
University of Basel
James T. Kirby
Professor
University of Delaware
Finn Lindgren
Professor
University of Edinburgh
Alessio Porretta
Professor
University of Rome Tor Vergata
Thordis Thorarinsdottir
Research Director
Norwegian Computing Center
Erik Wahlén
Senior lecturer
Lund University

person-portlet

Contact

Funding (IMod)

Funding

NFR Project number 325114

Activities (IMod)

Upcoming activities

Publications (IMod)

Publications

Wakefield, J., Gao, P., Fuglstad, G.-A., and Li, Z.R. (2025). The Two Cultures for Prevalence Mapping: Small Area Estimation and Model-Based Geostatistics. Statistical Science. In press.

Li, Z.R., Martin, B.D., Dong, T.Q., Fuglstad, G.-A., Paige, J., Riebler, A., Clark, S., and Wakefield, J. (2025). Space-Time Smoothing of Demographic and Health Indicators using the R Package SUMMER. The R Journal. In press.

Chowdhury, I., and Jakobsen, E.R. (2024) Precise Error Bounds for Numerical Approximations of Fractional HJB Equations. IMA J. Numer. Anal.. DOI: 10.1093/imanum/drae030. 

Chowdhury, I., Jakobsen, E.R., and Krupski, M. (2024) On fully nonlinear parabolic mean field games with examples of nonlocal and local diffusions. SIAM J. Math. Anal., 56(5):6302–6336.

Alibaud, N., Endal, J., and Jakobsen, E.R. (2024) Optimal stability results and nonlinear duality for L-infinity entropy and L1 viscosity solutions. J. Math. Pures Appl., 188:26–72.

Altay, U., Paige, J., Riebler, A., and Fuglstad, G.-A. (2024) GeoAdjust: Adjusting for Positional Uncertainty in Geostatistial Analysis of DHS Data. The R journal.

Weichert, S., Smeltzer, B. K., and Ellingsen, S. Å. (2023) Biases from spectral leakage in remote sensing of near-surface currents. IEEE Transactions on Geoscience and Remote Sensing.

Altay, U., Paige, J., Riebler, A., and Fuglstad, G.-A. (2022) Jittering Impacts Raster- and Distance-based Geostatistical Analyses of DHS Data. Statistical Modelling. In press.

del Teso, F., Endal, J., Jakobsen, E.R., and Vazquez, J.L. (2023) Evolution Driven by the Infinity Fractional Laplacian. Calc. Var.,  62(136).

del Teso, F., Endal, J., and Jakobsen, E.R. (2023) Uniform tail estimates and Lp-convergence for finite-difference approximations of nonlinear diffusion equations. Discrete Contin. Dyn. Syst., 43(3&4): 1319–1346.

Zhang, J., Bonas, M., Bolster, D., Fuglstad, G.-A., and Castruccio, S. (2023) High Resolution Global Precipitation Downscaling with Latent Gaussian Models and Nonstationary SPDE Structure. Journal of the Royal Statistical Society: Series C. In press.

Lenain, Luc; Smeltzer, Benjamin Keeler; Pizzo, Nick; Maria, Freilich; Colosi, Luke; Ellingsen, Simen Andreas Ådnøy; Grare, Laurent; Peyriere, Hugo; Statom, Nick. (2023) Airborne Remote Sensing of Upper-Ocean and Surface Properties, Currents and Their Gradients From Meso to Submesoscales. Geophysical Research Letters, 50.

Pizzo, Nick; Lenain, Luc; Rømcke, Olav; Ellingsen, Simen Andreas Ådnøy; Smeltzer, Benjamin Keeler. (2023) The role of Lagrangian drift in the geometry, kinematics and dynamics of surface waves. Journal of Fluid Mechanics, 954.

Smeltzer, Benjamin Keeler; Rømcke, Olav; Hearst, R. Jason; Ellingsen, Simen Andreas Ådnøy. (2023) Experimental study of the mutual interactions between waves and tailored turbulence. Journal of Fluid Mechanics, 962.

Zheng, Zibo; Li, Yan; Ellingsen, Simen Andreas Ådnøy. (2023) Statistics of weakly nonlinear waves on currents with strong vertical shear. Physical Review Fluids, 8.

Ehrnstrom, Mats; Nik, Katerina; Walker, Christoph. (2022). A direct construction of a full family of Whitham solitary waves. Proceedings of the American Mathematical Society, 151(2).

Ehrnstrom, Mats; Nik, Katerina; Walker, Christoph. (2022). A direct construction of a full family of Whitham solitary waves. Proceedings of the American Mathematical Society, 151(2).

Ehrnstrom, Mats; Nilsson, Dag; Groves, Mark D. (2022) Existence of Davey–Stewartson type solitary waves for the fully dispersive Kadomtsev–Petviashvilii equation. SIAM Journal on Mathematical Analysis, 54(4).

Ehrnstrom, Mats; Wang, Yuexun. (2022) Enhanced existence time of solutions to evolution equations of Whitham type. Discrete and Continuous Dynamical Systems. Series A, 42(8).

Paige, J., Fuglstad, G.-A., Riebler, A., and Wakefield, J. (2022). Spatial Aggregation with Respect to a Population Distribution: Impact on Inference. Spatial Statistics, 52.

Preprints (IMod)

Preprints

Auestad, Ø.S., Fuglstad, G.-A., Jakobsen, E.R., and Lang, A.. (2025) Finite element approximation of parabolic SPDEs with Whittle–Matérn noise. arXiv:2406.11041.

Auestad, Ø.S.. (2024) Numerical approximation of linear parabolic evolution equations revisited. arXiv:2406.02796.

person-portlet

Junior researchers

person-portlet

Affiliated researchers

Footer spacing (ESGI)